• 3D optical lens system ray trace analysis.
• 3D far-field modeling of truncated Gaussian optical beams.

3D optical lens system ray trace analysis.

This section under construction – please check back later.


Top of Page

3D far-field modeling of truncated Gaussian optical beams

It is often useful to know the far-field radiation pattern of specific types of optical beams. The far-field pattern for an arbitrary beam may be numerically calculated if the beam intensity and phase is assumed to be defined over a flat, rectangular, ‘entrance’ aperture (located at z=0). The beam intensity is assumed to be zero everywhere outside this entrance aperture (the aperture is zero-baffled). 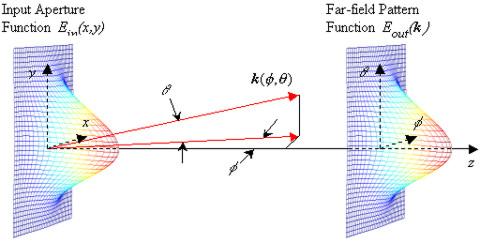Figure 1 illustrates the geometry of the problem.

Figure 1. Assumed geometry of the far-field extrapolation problem

Given the complex aperture function E_in(x,y), the far-field pattern E_out(k) is a function of the direction angles Φ,Θ as well as the wavelength λ. Specifically, E_out(k) is a 2D Fourier transform of the aperture function E_in(x,y),

Eq. 1 is based on Fraunhofer diffraction theory which assumes that the far-field pattern is projected sufficiently far away from the input aperture. Taking the aperture diameter to be D, and the distance between the aperture and the output screen to be R, the Fraunhofer criterion is that R >> D²/(8λ). For engineering purposes, this criterion is often simplified to R > D²/λ. For example, assuming D = 100 μm for a collimated fiber optic beam, and taking λ = 1.5 μm, then the Fraunhofer criterion is approximately R > 0.7 cm.

It is obviously possible to compute the transform integral (Eq. 1) using 2D fast Fourier transforms. An alternative approach is to model the function E_in(x,y) over the input aperture with continuous polynomials. In the examples below, the real and imaginary parts of E_in(x,y) were modeled with bicubic splines. The real part of E_in(x,y), for example, was modeled over the input aperture as:

(2)

Plugging this expression (along with the imaginary part) into Eq. 1, the integral can then be computed to third order in closed form over each x_i,y_j element of the input aperture. This element-by-element summation is repeated for each far-field direction in which the far-field solution is sought.

The accuracy of this method depends on how well the input grid samples the aperture function. I have found that the results are generally quite accurate even for sparsely sampled input functions. The smoothness of the aperture function over the input grid determines how well-sampled the function is. If the successive derivatives of the interpolating splines decrease rapidly in magnitude, then truncating the integration at third order produces very small errors.

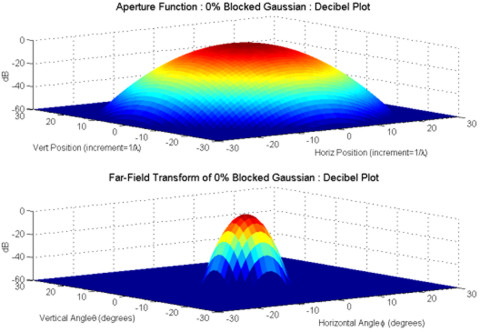
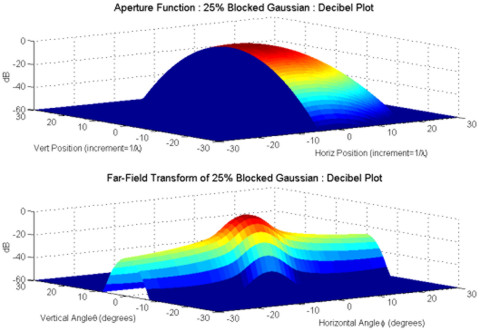
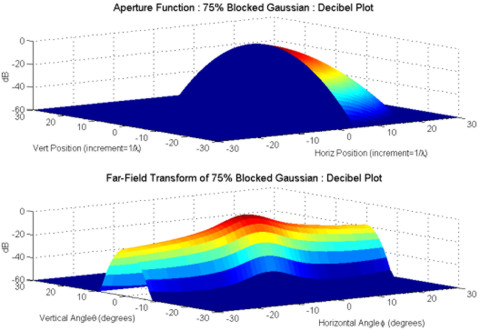
The following examples illustrate computed far-field patterns of a Gaussian input beam blocked by a knife-edge occlusion to various extents. Decibel plots of the input aperture and the resulting far-field distributions are shown for 0%, 25%, and 75% blocked Gaussian beams. Amplitudes in these plots have been truncated at a decibel ‘floor’ of –60 dB (values below –60 dB are plotted as –60 dB). Note that the coordinates of the input aperture plots are in units of (non-dimensionalized) distance (grid distance divided by wavelength), while the coordinates of the far-field distribution plots are in degrees (angles).

Top of Page